Alarm! 570 księży pedofilów idzie po nasze dzieci!

Zagadnienia matematyczne [Zbigniew P. Szczęsny]:

Zagadnienia obliczania prawdopodobieństwa zdarzeń sprowadzają się często do obliczenia tego, na ile sposobów dane zdarzenie można zrealizować. Zauważmy bowiem, że wybierając na przykład losowo pojedynczą kulę z naczynia, w którym znajdują się dajmy na to trzy kule czarne i dwie białe – kulę czarną możemy wybrać na trzy sposoby a kulę białą już tylko na dwa.

Łatwiej to zrozumieć, jeśli przyjmiemy, że kule są dyskretnie ponumerowane i numery od jeden do trzech przypadły kulom czarnym a numery od czterech do pięciu – kulom białym. Wówczas zdarzenie polegające na wylosowaniu kuli czarnej możemy zrealizować wybierając kulę numer 1, 2 lub 3, podczas gdy wylosowanie kuli białej jest możliwe jedynie poprzez wybranie kuli nr 4 lub 5. Natomiast zdarzenie polegające na wybraniu jakiejkolwiek kuli możemy zrealizować już na pięć sposobów wybierając kulę o numerze 1, 2, 3, 4 lub 5.

Prawdopodobieństwo wybrania kuli czarnej obliczymy dzieląc ilość sposobów wybrania kuli czarnej przez ilość sposobów wybrania kuli dowolnej. W naszym przypadku wyniesie ono zatem 3/5 = 0,6, podczas gdy prawdopodobieństwo wybrania kuli białej 2/5 = 0,4. Mamy więc półtora raza więcej szans na wybranie kuli czarnej niż białej.

Ogólnie, ilość sposobów wybrania k elementów ze zbioru n elementów opisany jest wyrażeniem matematycznym znanym jako tzw. dwumian Newtona:

Znak wykrzyknika oznacza tu specjalną funkcję o nazwie silnia, której wartość wylicza się mnożąc kolejno przez siebie liczby od 1 do n:

n! = 1* 2 * 3 * 4 … * n

Silnia jest funkcją bardzo szybko rosnącą. Liczba będąca silnią ze stu ma już aż 157 cyfr! Oznacza to, wyliczanie silni z dużych liczb jest sporym problemem obliczeniowym.

Zobaczmy dla przykładu na ile sposobów można wybrać dwie kule spośród pięciu:

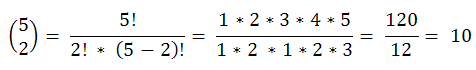Zauważmy, że dokładnie taką samą wartość otrzymamy dla wybierania trzech kul spośród pięciu:

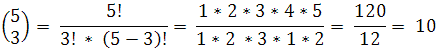Czemu tak? – To proste – wjęcie z klosza dwóch kul oznacza to samo, co pozostawienie w nim trzech! Czyli można przez proste przeformułowanie zadania stwierdzić, że liczba sposobów wybrania k elementów ze zbioru n elementowego jest taka sama, jak liczba sposobów wybrania n – k lementów ze zbioru n elementowego. Zatem:

Graficznie zwykło przedstawiać się to spostrzeżenie za pomocą tzw. trójkąta Pascala, gdzie wartości dwumianowe umieszcza się w kształcie piramidy, której każdy wyraz jest sumą dwóch znajdujących się dokładnie nad nim:

czyli

Jak zatem wyznaczyć prawdopodobieństwo zdarzenia polegającego na tym, że wśród na przykład dziesięciu kul wybranych z urny, w której umieszczono 20 kul czarnych i 10 kul białych, znajdą się dokładnie cztery kule białe i sześć czarnych? Liczymy:

Liczba sposobów wybrania dowolnych 10 kul spośród 30 kul wynosi:
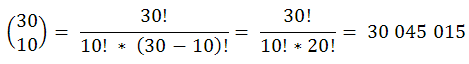Liczba sposobów wybrania 4 białych kul spośród 10 białych wynosi:

Liczba sposobów wybrania 6 czarnych kul spośród 20 czarnych wynosi:

A zatem liczba sposobów wybrania 4 białych kul i 6 czarnych z urny, w której było 20 kul czarnych i 10 kul białych wynosi: 210 * 38 760 = 8 139 600, gdyż dla każdego określonego sposobu wyboru kul białych mamy 38 760 możliwości wyboru kul czarnych.

Prawdopodobieństwo wybrania z urny dokładnie 4 kul białych i 6 czarnych wynosi zatem:

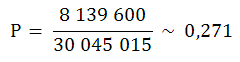Jeśli będziemy liczyć prawdopodobieństwo wylosowania każdej pojedynczej kombinacji, to wyniki ułożą się na krzywej zwanej rozkładem prawdopodobieństwa.

Zbadajmy rozkład prawdopodobieństwa dla naszego przykładu losowania 10 kul z urny, w której znajduje się 10 kul białych i 20 kul czarnych:

Wylosowanych białych kul	0	1	2	3	4	5
P	0,006	0,056	0,189	0,310	0,271	0,130
Wylosowanych białych kul	6	7	8	9	10	–
P	0,034	0,004	<0,001	<0,001	<0,001	–

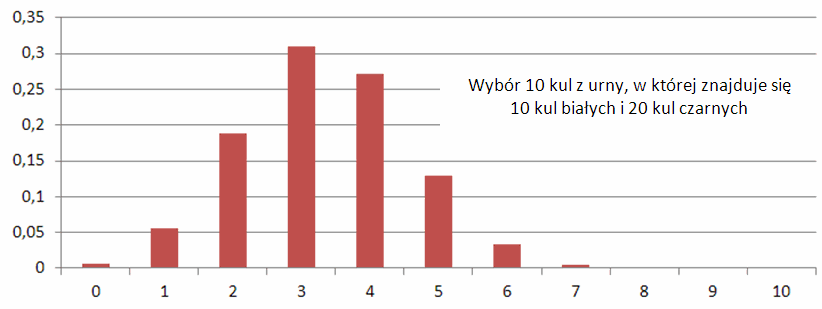Łatwo zauważyć, że suma wartości P w dolnym rzędzie (z dokładnością do zaokrągleń) wynosi 1, co oznacza, że pewnym jest, iż losując dziesięć z urny 10 kul znajdziemy wśród nich od 0 do 10 kul białych – innej możliwości po prostu nie ma. Jest to prawidłowość ogólna – prawdopodobieństwa pokrywające pełny zakres wszystkich możliwości muszą sumować się do jeden.

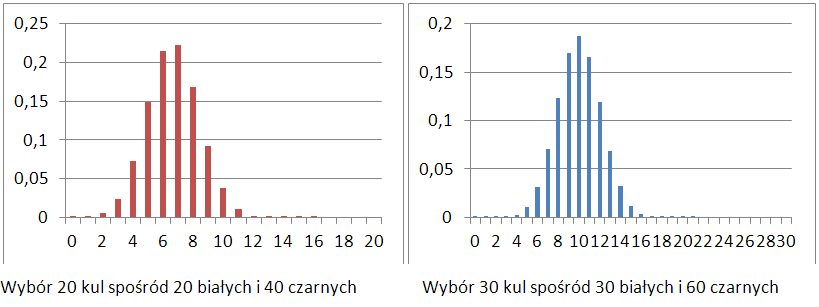
Podczas zwiększania liczby kul przy zachowaniu stosunku ilości kul białych do czarnych charakterystyczny dzwonowy kształt krzywej rozkładu prawdopodobieństwa staje się coraz bardziej widoczny:

Spróbujmy teraz policzyć coś naprawdę ciekawego
(dane liczbowe wzięte z Wikipedii):

• Liczba księży i zakonników katolickich (kizk) na świecie:
  n = 413 400
• Liczba kizk pedofilów na świecie: y = 0,02 * n = 8 268
  (papież Franiszek powiedział w wywiadzie dla włoskiego dziennika La Repubblica, że wśród księży na świecie jest dwa procent pedofilów)
• Liczba kizk nie-pedofilów na świecie: w = n – y = 405 132
• Liczba kizk w Polsce: k = 28 500

Zbadajmy teraz jakie jest prawdopodobieństwo, że wśród polskich księży i zakonników katolickich znajdzie się również 2% pedofilów:

• Liczba polskich kizk pedofilów: t = 0,02 * k = 570
• Liczba polskich kizk nie-pedofilów: z = k – t = 27 930

Wyznaczmy zatem:

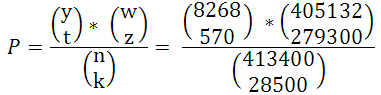
Jak już pisałem, wyliczanie silni z dużych liczb jest obliczeniowo bardzo trudne, gdyż funkcja ta jest niezwykle szybko rosnąca i wyznaczane wartości szybko przekraczają możliwości maszyn matematycznych. W związku z tym, dwumian Newtona dla dużych liczb wyznacza się nie wprost, lecz korzystając z właściwości logarytmów naturalnych oraz wprowadzonej do matematyki przez wielkiego osiemnastowiecznego matematyka niemieckiego Leonarda Eulera funkcji specjalnej, tzw. funkcji gamma oznaczanej literą grecką Γ. W zapisie tym mamy:

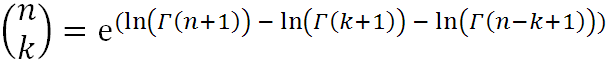
Przy czym symbol e oznacza podstawę logarytmu naturalnego.

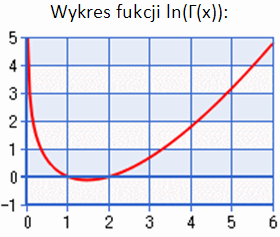Wartości funkcji ln(Γ(x)) dla dużych x można wyznaczyć korzystając z kalkulatora umieszczonego na tej stronie internetowej.
Wartości funkcji e^x dla bardzo dużych x można wyznaczyć korzystając z kalkulatora umieszczonego na tej stronie internetowej.

Korzystając z powyższych narzędzi mamy dla dwumianu:

• Wartość pierwszego wyrażenia logarytmicznego w wykładniku:
  4 932 766,846
• Wartość drugiego wyrażenia logarytmicznego w wykładniku:
  263 849,340
• Wartość trzeciego wyrażenia logarytmicznego w wykładniku:
  4 565 205,729
• Różnica tych trzech wyrażeń: 103 711,777
• Wartość fukcji e^x dla x jak powyżej: 2.8344E+45041

Jak widać wyszła ogromna liczba o ponad czterdziestu pięciu tysiącach cyfr!

Wyliczając w podobny sposób pozostałe dwumiany i dzieląc odpowiednio otrzymane wartości otrzymujemy interesujące nas prawdopodobieństwo: P = 0,01749 ≈ 0,0175 = 1,75%.

Nie powinno nas dziwić, że otrzymany wynik jest tak niewielki – wszak obliczyliśmy wartość prawdopodobieństwa, że wśród polskich księży i zakonników katolickich jest dokładnie 570 pedofilów a przecież prawdopodobieństwo, iż jest ich na przykład 569 czy 571 nie może być znacząco różne. Żeby ocenić przebieg krzywej rozkładu i znaleźć zakres, w którym osiąga ona maksimum powinniśmy wyznaczyć wartość prawdopodobieństwa w kilku punktach wokół wartości 570.

Sporządźmy tabelkę prawdopodobieństwa znalezienia się w Polsce określonego procenta pedofilów wśród księży i zakonników katolickich (używam notacji naukowej gdzie 0,0175 = 1,75E-02):

%	1,50	1,75	1,80	1,85	1,90	1,95	2,00
P	1,42E-11	1,20E-04	7,30E-04	2,94E-03	8,32E-03	1,46E-02	1,75E-02
%	2,05	2,10	2,15	2,20	2,25	2,50	–
P	1,44E-02	7,72E-03	2,97E-03	8,07E-04	1,55E-04	1,73E-10	–

A następnie na jej podstawie sporządźmy wykres rozkładu tego prawdopodobieństwa:

Jak widać, ponieważ wartości prawdopodobieństwa dla przedziałów spoza zakresu 1,80..2,20 są zupełnie znikome, to z prawdopodobieństwem graniczącym z pewnością (P > 0,99) można powiedzieć, że jeśli papież Franciszek powiedział prawdę, to mamy w Polsce właśnie od 513 (1,8% z 28 500) do 627 (2,2% z 28 500) księży i zakonników pedofilów, co wydaje się bardzo poważnym problemem kryminalnym wymagającym jakiejś interwencji państwa.